For over 60 years, a geometry problem has been puzzling scientists. Scientists have struggled to find a geometric shape that does not repeat itself when tiled.
This elusive shape is known to mathematicians as ‘Einstein’, a clever pun from the German words Ein and Stein which means one stone.
This decades-long geometry problem has been solved!
The discovery was largely the work of David Smith, a tiling enthusiast from Yorkshire, England who discovered a 13-sided shape nicknamed ‘The Hat’. This unique 13-sided shape can be arranged in tile formation forever, and it will never repeat a pattern or never can be made to repeat.
Smith had been experimenting with paper cut-outs of shapes but that can only be tested with a finite plane. To confirm the Hat’s special abilities, he collaborated with Craig S. Kaplan, associate professor of computer science from the University of Waterloo in Canada. Kaplan could check a given shape on larger scales on his recently developed software.
From 20,426 shapes to one…how has the aperiodic tiling been achieved?
Aperiodic tiling, or a tiling pattern that does not repeat itself has been achieved in the past too.
But it has either used multiple shapes and after a certain point, patterns will start repeating themselves.
In the 1960s, the first aperiodic tile set was created using 20,426 different shapes. In 1974, British physicist and Nobel Prize winner Roger Penrose made an aperiodic tiling set using two different rhombus shapes and that’s where the things got stuck for decades.
A 60-Year Mathematical Mystery Solved With ‘Einstein’ Shape That Does Not Repeat Itself When Tiled
By: | April 19th, 2023
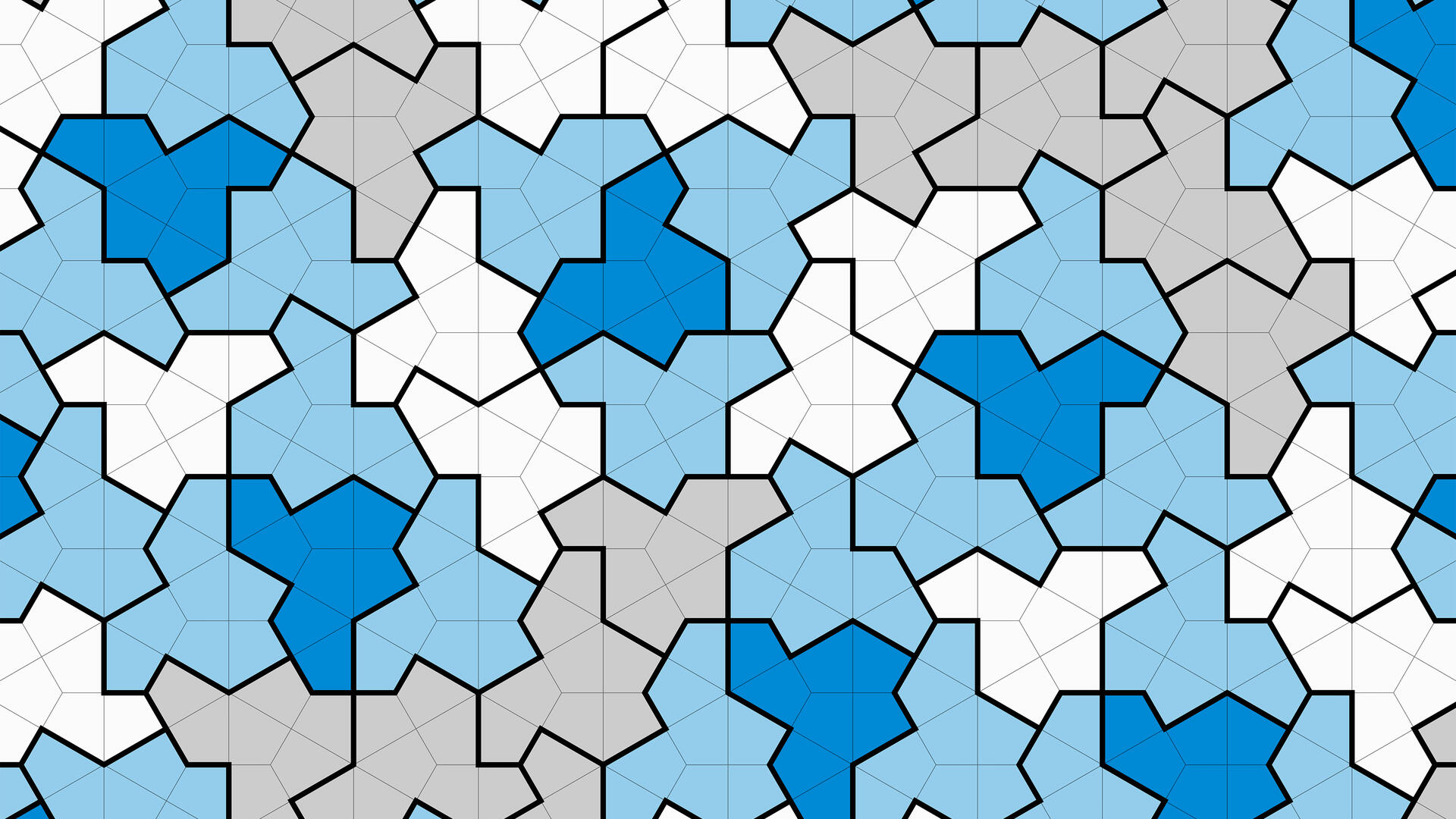
Image by University of Waterloo
More articles from Industry Tap...