On April 1, 2017, a Silicon Valley startup named Apollo Fusion announced its intention to create a fusion-fission hybrid power plant [3]. The company consists of two key people: a plasma thruster expert and an audacious internet entrepreneur. Both are pictured below [2,4]. The entrepreneur is Mike Cassidy.
Key Personnel
Mr. Cassidy is a big deal. His name alone, makes this company one to watch. Most recently, Cassidy served as an executive director, at Google. He has lead and sold off multiple companies since starting in business in the early nineties [5]. In a word he is a classic Silicon Valley entrepreneur. The man is also well connected: Tech Crunch has reported that Larry Page and Sergey Brin of Google are both “super enthusiastic” about this startup [1]. The other person involved is Dr. Ben Longmier. Dr. Longmier is currently an adjunct professor of aerospace engineering at the University of Michigan [4]. He has worked extensively, in plasma thrusters.
Until April 4, 2017, I had never heard of either of these guys. They both work in different fields from traditional fusion. Whatever the case may be, we need them; the quest for fusion power needs all the help it can get.
Apollo Fusion’s Patent Application
I was able to get a hold of Apollo Fusions’ patent application [7]. It was filed on September 1, of 2015. I would guess that Dr. Longmier spearheaded this effort and brought Mike Cassidy in later. The company’s approach is based on plasma thruster research. Their concept reminds me most of a virtual cathode made inside a penning trap. That idea was originally suggested by Dan Barnes, of the Los Alamos National Labs, back in 2000 [23]. In any case, the gist of it is: get a lot of electrons together and have them attract ions towards one spot. Get them moving at high enough speeds to create fusion. That sounds a lot like a polywell.
Plasma Thruster Research
Dr. Longmier is lucky to work in plasma thruster research. Indeed, they may be better understood than traditional fusion devices. Thrusters have gotten the funding, while our fusion field has languished. Your basic thruster relies on the Hall Effect. This is a well-researched topic with roots back into the sixties [7]. Multiple research teams have been involved in this effort, over the past five decades and Hall Thrusters have been used to circle the moon [6].
A Basic Thruster
How do plasma thrusters work? They are normally tested in low pressure vacuum environments (1.3E-3 to 1.3E-6 Pascal). In the past, these thrusters sat on large satellites, but there has been a recent push into smaller, cube stats. A cube stat is a hunk of metal, 10 centimeters to a side. They represent the next generation of satellites. This change is reflected in Dr. Longmiers’ research. On paper, he is part of the University of Michigans’ Plasmadynamics and Electric Propulsion lab. That lab was founded in 1992 and since then, has hosted 15 or 20 big thruster experiments [9]. They were all housed inside a vast, 200 cubic meter tank. These represent the old kind of thrusters. Dr. Longmier has pushed into smaller sizes [24]. He has focusing on cube stats. The basic mechanism of a Hall thruster is shown below [8, 6].
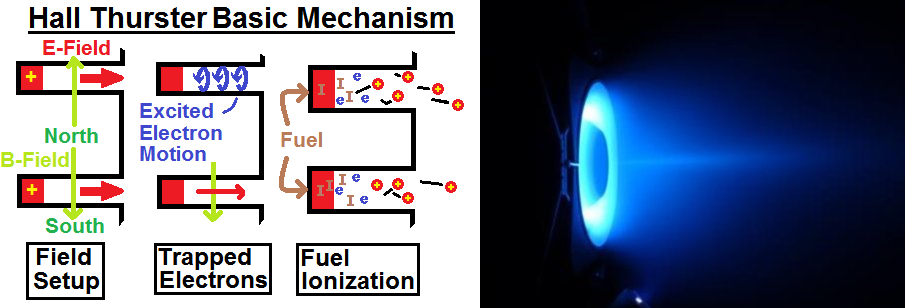
Hall Thruster Basic Mechanism (Image Courtesy http://www.thepolywellblog.com/)
How To Build, Set Up a Hall Thruster
To build a hall thruster, the first thing you need to do is set up your fields. At the center of the thruster is a ringed cavity. This is filled with both a magnetic and electric field. These fields run perpendicular, to one another. The magnetic field comes out from the center, while the electric field points out from the bottom of the cavity. The Lorentz force dictates electrons inside this cavity will mostly stay there. Once set up, you need to light your thruster. To do this, you must inject a fuel. Xenon is the most common fuel to burn. This is because it is a big fat atom that is easy to ionize. The Xenon atoms interact with the electrons and ionize. Once positive, they fly away from the positive electric field. When they leave this cavity they accelerate, pushing the satellite forward. As they fly, they suck in electrons which neutralize the beam. This makes a broad, neutral jet, pushing the satellite forward.
Comparing Apollo Fusion with Traditional Fusion Research
The biggest differences between this kind of work and traditional fusion research is the scale of everything. For example, the magnetic fields used inside a hall thruster will only reach a few hundred guass [10]. Meanwhile, a polywell will need a field that is 80 times higher [11]. These are the kind of fundamental differences, which change everything about how you do your testing. For example, a Hall thruster could be run for several minutes, powered by batteries or the wall outlet. In stark contrast, the Lockheed fusion reactor must run off capacitors. Hence, Lockheed can only fire their machine for a few microseconds [12-14].
Another difference is the plasma temperature. Thruster plasma is tens of electronvolts, aka very cold. A typical fusor does fusion at 30,000 eletronvolts or hotter [15, 16]. That difference is stark, and it effects everything about how the plasma behaves. Finally, the fuels are very different. Xenon is easy to use. It is a noble gas, which works well in a vacuum system. Vacuum experts say you need a noble gas to push out the air in a Vacuum [26]. A fusion fuel like tritium is very different. When we worked with it at the Laboratory for Laser Energetics, it was a cost, regulatory and safety hassle.
If Apollo Fusion wants to burn tritium, they will need a great deal more technical staff and costs.
All this being said, Dr. Longmier has a history of pushing the bounds of technology. He was part of a team that developed a 200 kilowatt rocket engine at the Ad Astra Rocket Company, in Houston [18]. As I understand it, this is an order of magnitude better than other rocket thrusters. This company is widely known in the space community, because of its’ CEO, Dr. Franklin Chang Díaz. Reaching such a high thrust means that many other plasma parameters and field strengths should rise in kind. But here is the key question: would plasmas in rockets get so good that they could start to look like fusion plasmas?
About Apollo Fusion, Inc.’s Patent
Patents are always vague. At first glance, this concept looks like an electron jet, inside some bigger fields. At its core is an electron beam. This beam runs right through the center of the machine. The idea is to get the electrons in this beam to bunch together. This, in turn, will attract the ions for fusion reactions. The patent does not mention how they plan to make this electron beam. But they will need some solution here. If the electrons are not shoved forward with enough kick, they will be scattered by the other fields inside this machine. Fortunately, there are several off the-shelf electron beams that they can buy [19]. Once shot forward, the electrons will encounter several other fields simultaneously.
Normally, I would model these fields, as I have in the past for the polywell and Lockheeds’ CFR [20, 21]. A model is very straightforward. You use excel, Newtons’ equations of motions and the Lorentz force to map out how the electrons move around. If you want to get fancy, you use MATLAB or COMSOL. Regrettably, this patent gives us no hint as to the field strengths or dimensions inside this machine. The picture that they do give, is reproduced below [7].
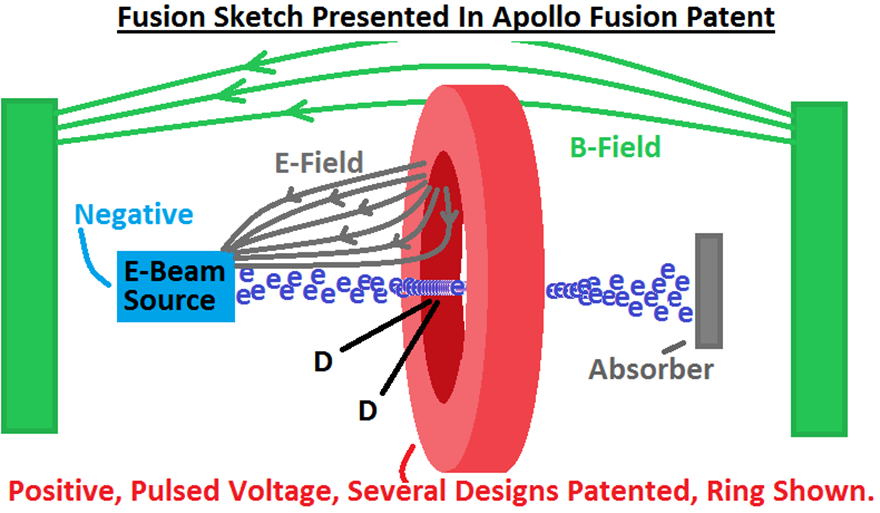
Apollo Fusion Patent Sketch (Image Courtesy http://www.thepolywellblog.com/
Analyzing Apollo Fusions Inc.’s Patent Diagram
This is a very busy picture. The first thing you notice the large green field on the outside. This is supposed to be a balanced magnetic field. Ideally, this opposes the electron beam [7]. The patent promises that this magnet should slow the electron leakage to the ring in the center. The next thing that you notice is that big red ring. That is just one big, positive voltage ring. A positive lump metal, for which the design is not finalized. The patent, in fact, covers several ring designs. The patent claims that if you pulse a voltaage on this ring, you can increase the plasma density in the electron beam by 700 fold. Where is this claim coming from? It be must from one of Dr. Longmiers’ publications.
The center of that ring, is where the magic happens. This increase in beam density is support to pull ions in towards the center. If everything works as planned, the ions will slam together and fuse. This will generate neutrons, which will fly away and hit the walls. The patent then talks about using FLiBe, in the walls, to absorb the neutrons. FLibe is a popular molten salt which has been pushed by the thorium community [22]. This would represent a fusion-fission hybrid approach.
Assessment of Apollo Fusion, Inc.’s Patent
Obviously, this patent and Apollos’ website will not reveal how far along this research is. Since the patent was filed in 2015, it is safe to say that Longmier has been looking at this problem for some years. That said, he has a full time job, so he does not have infinite time to develop the idea. This concept is similar to many other fusion devices – it looks like a tuning problem. You have several parameters that you can adjust. These include, but are not limited to: the fuel injection rate, the shape of the electrode, the vacuum pressure (1E-5 to 1E-10 torr), both the field strengths and their positions.
You can also change the beam characteristics and how everything is placed in the machine. As you adjust these parameters, you toggle between effects that you love and effects that you aren’t working. One bad effect might be electrons leaving the beam and going somewhere undesirable. Another effect could arise from the transient nature of the voltage that is pulsed. Plasma can escape when fields change. Finally, there is the issue of squashing the material together. We know there are limits to how dense you can squash a plasma [25]. Ultimately, the goal would be to “tune” this design to increase the fusion rate and dial down everything else.
An experienced researcher will know how to do that. Using models and dimensionless numbers, they will try to map out these modes of operation, for this machine. But once that is all done, Apollo will need to figure out how to scale it up. They will also need to find a way to make regulators (like the US Nuclear Regulatory Commission) happy. In any case, it looks like Apollo Fusion has a long road ahead of it.
If you have questions for Dr. Matt
Citations
1. Heater, Brian. “Google’s Project Loon Head Is Getting into Nuclear power.” TechCrunch. TechCrunch, 03 Apr. 2017. Web. 05 Apr. 2017. <https://techcrunch.com/2017/04/03/googles-project-loon-head-is-getting-into-nuclear-power/>.
2. Stone, Brad. “Former Google Vice President Starts a Company Promising Clean and Safe Nuclear Energy.” Bloomberg.com. Bloomberg, 03 Apr. 2017. Web. 05 Apr. 2017. <https://www.bloomberg.com/news/articles/2017-04-03/former-google-vice-president-starts-a-company-promising-clean-and-safe-nuclear-energy>.
3. Cassidy, Mike, and Ben Longmier. “Apollo Fusion.” Apollo Fusion. Apollo Fusion, 01 Apr. 2017. Web. 05 Apr. 2017. <http://apollofusion.com/>.
4. “Benjamin Longmier.” Michigan Engineering Faculty. University of Michigan, n.d. Web. 05 Apr. 2017. <http://www.engin.umich.edu/college/about/people/profiles/k-to-o/benjamin-longmier>.
5. “Mike Cassidy (entrepreneur).” Wikipedia. Wikimedia Foundation, 04 Apr. 2017. Web. 05 Apr. 2017. <https://en.wikipedia.org/wiki/Mike_Cassidy_(entrepreneur)>.
6. “Hall-effect Thruster.” Wikipedia. Wikimedia Foundation, 05 Apr. 2017. Web. 05 Apr. 2017. <https://en.wikipedia.org/wiki/Hall-effect_thruster>.
7. Longmier, Ben. Hall Effect Assisted Electron Confinement in an Inertial Electrostatic Confinement Fusion Reactor. Apollo Fusion, Inc., assignee. Patent US 2017/0069399 A1. 09 Mar. 2017. Print.
8. “Sekerak, Michael J., Alec D. Gallimore, Daniel L. Brown, Richard R. Hofer, and James E. Polk. “Mode Transitions in Hall-Effect Thrusters Induced by Variable Magnetic Field Strength.” Journal of Propulsion and Power 32.4 (2016): 903-17. Web.
9. Lobbia, Robert. “About the Plasmadynamics and Electric Propulsion Laboratory.” The Plasmadynamics and Electric Propulsion Laboratory. University of Michigan, n.d. Web. 05 Apr. 2017. <http://pepl.engin.umich.edu/about.html>.
10. Hofer, Richard R., and Alec D. Gallimore. “High-Specific Impulse Hall Thrusters, Part 2: Efficiency Analysis.” Journal of Propulsion and Power 22.4 (2006): 732-40. Web. 5 Apr. 2017. <https://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/20040084644.pdf>.
11.https://www.fpds.gov/ezsearch/search.do?indexName=awardfull&templateName=1.4.3&s=FPDSNG.COM&q=energy%2Fmatter&sortBy=SIGNED_DATE&desc=Y
12. Moynihan, Matthew. “An Intensive Analysis Of Fusion Research At Lockheed Martin.” N.p., 11 Dec. 2016. Web. 5 Apr. 2017. <https://www.linkedin.com/pulse/intensive-analysis-fusion-research-lockheed-martin-moynihan>.
13. Park, Jaeyoung, Nicholas A. Krall, Paul E. Sieck, Dustin T. Offermann, Michael Skillicorn, Andrew Sanchez, Kevin Davis, Eric Alderson, and Giovanni Lapenta. “High-Energy Electron Confinement in a Magnetic Cusp Configuration.” Physical Review X 5.2 (2015): n. pag. Web. 5 Apr. 2017. <https://journals.aps.org/prx/abstract/10.1103/PhysRevX.5.021024>.
14. Kowch737. “New Generation of Engines.” YouTube. European Space Agency, 02 Mar. 2010. Web. 05 Apr. 2017. <https://www.youtube.com/watch?v=H7Q5khg87aU>.
15. “A Conversation with Carl Greninger.” Private interview, by Matt Moynihan and Carl Greninger. 22 Aug. 2016
16. Bakdemir, A. S., Y. Akgn, and A. Alak. “Preliminary Results of Experimental Studies from Low Pressure Inertial Electrostatic Confinement Device.” Journal of Fusion Energy 32.5 (2013): 561-65. Web. 5 Apr. 2017.
17. Lobbia, Robert. “Personnel.” The Plasmadynamics and Electric Propulsion Laboratory. University of Michigan, n.d. Web. 05 Apr. 2017. <http://pepl.engin.umich.edu/personnel.html>.
18. https://arc.aiaa.org/doi/abs/10.2514/1.B34801 Improved Efficiency and Throttling Range of the VX-200 Magnetoplasma Thruster
19. LAPEDUS, MARK. “Multi-Beam Market Heats Up.” Semiconductor Engineering. Semiconductor Engineering, 17 Mar. 2017. Web. 05 Apr. 2017. <http://semiengineering.com/multi-beam-market-heats-up/>.
20. “The Serious Need For Data.” The Serious Need For Data. The Polywell Blog, 06 Jan. 2014. Web. 05 Apr. 2017. <http://www.thepolywellblog.com/2014/01/the-serious-need-for-data.html>.
21. “The Physical Basis For The Polywell.” The Physical Basis For The Polywell. The Polywell Blog, 30 July 2012. Web. 05 Apr. 2017. <http://www.thepolywellblog.com/2012/07/the-physical-basis-for-polywell.html>.
22. Sorensen, Kirk. “Flibe Energy.” Flibe Energy. N.p., n.d. Web. 05 Apr. 2017. <http://flibe-energy.com/>.
23. Barnes, D. C., M. M. Schauer,K. R. Umstadter, L. Chacon, and G. Miley. “Electron Equilibrium andConfinement in a Modified Penning Trap and Its Application to PenningFusion.” Physics of Plasmas Phys. Plasmas 7.5 (2000): 1693. Web. 22 May2016..
24. Longmier, Ben. “Plasma Ambipolar Thrusters.” YouTube. Michigan Engineering, 25 Feb. 2014. Web. 05 Apr. 2017. <https://www.youtube.com/watch?v=Fcr-ZVuJYzU>.
25. Caflisch, R. E., and M. S. Rosin. “Beyond the Child-Langmuir Limit.” Physical Review E. American Physical Society, 18 May 2012. Web. 05 Apr. 2017. <https://journals.aps.org/pre/abstract/10.1103/PhysRevE.85.056408>.
26. “Vacuum Particles: Does pumping noble gases require special considerations?” Edwards Vaccuums. Web. 06 Apr. 2017. <http://www.edwardsvacuum.com/asia/newsletters/particles/0914/ask_en.html>.